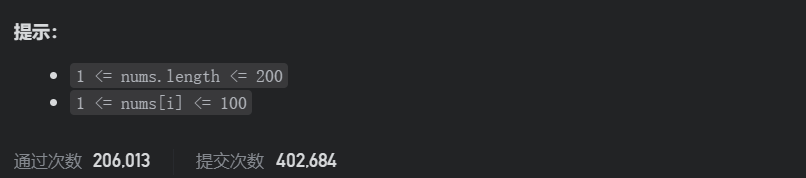
题目

leetcode:416

代码与解析

背包问题

carl: 背包问题01
carl:背包问题 滚动数组法

题目解析

讲解最清晰版
官方视频题解

动归五部曲

• 确定dp数组下标及含义

在01背包中，dp[j] 表示： 容量为j的背包，所背的物品价值最大可以为dp[j]。dp[i][j]

套到本题，dp[j]表示 背包总容量是j，最大可以凑成j的子集总和为dp[j], dp[i]为每一个元素。

• 确定递推公式

dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i])

• dp数组初始化

这里采用二维数组，初始化的话，第一列初始化为零，每一行要看j是否大于nums[i]， 装不下的话，当前格就不能装。

if j<nums[i]{
    dp[i][j] = dp[i-1][j]
}else{
    dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i])
}

• 确定遍历顺序

遍历顺序的话，从前往后遍历，可以先遍历背包，也可先遍历物品

• 举例推导dp数组

[
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 5 5 5 5 5 5 5]
[0 0 0 0 0 5 5 5 5 5 5 11]
[0 0 0 0 0 5 5 5 5 5 10 11]
]

func canPartition(nums []int) bool {
    target := sum(nums)
    if target%2 !=0{
        return false
    }
    target = target/2
    dp := make([][]int, len(nums))
    for i:=0;i<len(nums);i++{
        dp[i] = make([]int, target+1)
        dp[i][0] = 0
    }
    // fmt.Println(dp)
    for i:=1;i<len(nums);i++{
        for j:=0;j<=target; j++{
            if j<nums[i]{
                dp[i][j] = dp[i-1][j]
            }else{
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i])
            }
        }
    }
    fmt.Println(dp)
    return dp[len(nums)-1][target] == target
}
func sum(nums []int)int{
    temp := 0
    for _, v :=range nums{
        temp += v
    }
    return temp
}

滚动数组版本

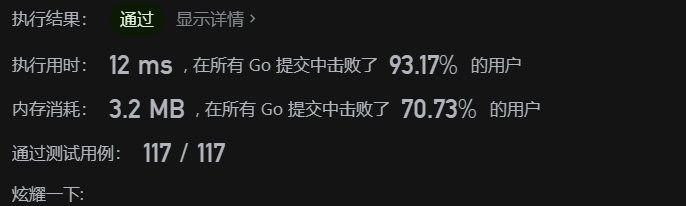
func sum(nums []int)int{
    temp := 0
    for _, v :=range nums{
        temp += v
    }
    return temp
}
func max(m, n int)int{
    if m>n{
        return m
    }
    return n
}
func canPartition(nums []int) bool{
    target := sum(nums)
    if target%2 !=0{
        return false
    }
    target = target/2
    dp := make([]int, target+1)
    for i:=1;i<len(nums);i++{
        for j:=target;j>=nums[i];j--{
            dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])
        }
    }
    // fmt.Println(dp)
    return dp[target]==target
}