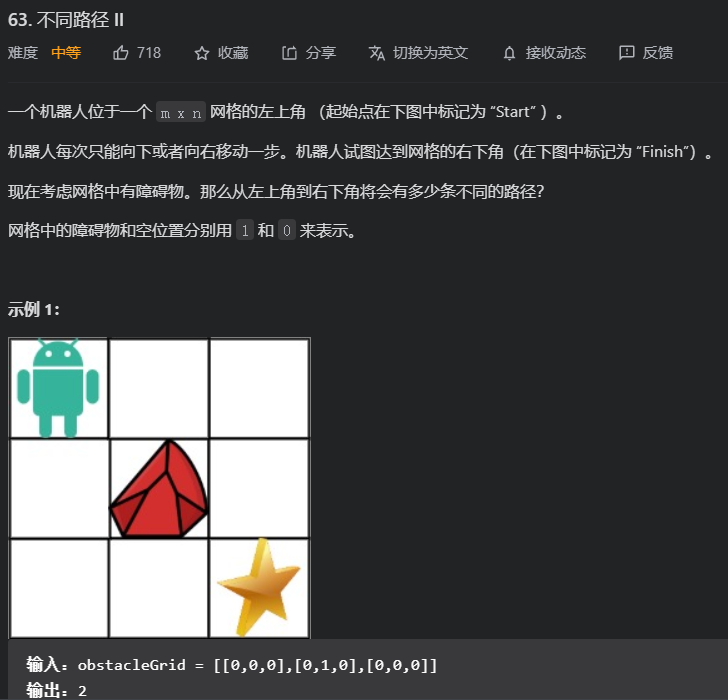
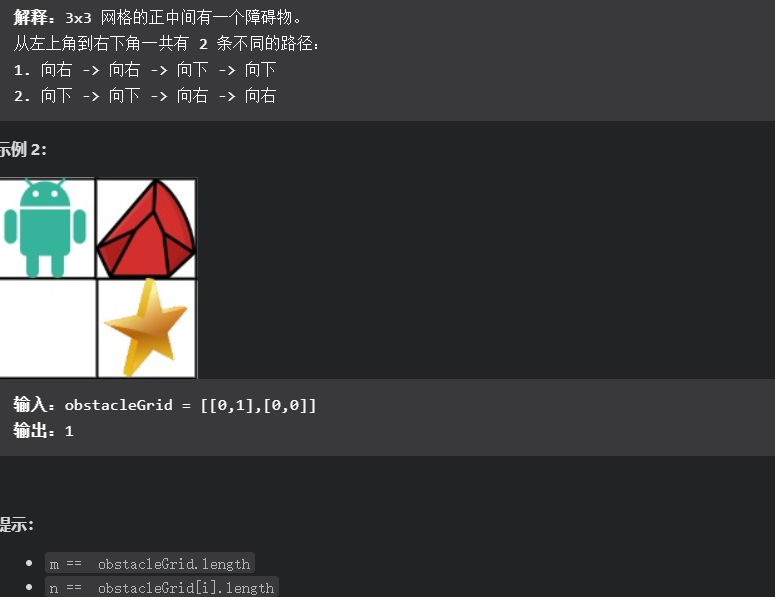
题目

leetcode:63

代码与解析

这道题和上一道有点像

动归五部曲

• 确定dp数组下标及含义
  dp用来存放从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

• 确定递推公式

在遍历dp的时候也遍历给定的数组，同步遍历
如果当前节点不为1，那么

dp[i][j] = dp[i-1][j]+dp[i][j-1]

• dp数组初始化

m,n:= len(obstacleGrid),len(obstacleGrid[0])
// 定义一个dp数组
dp := make([][]int,m)
// 初始化dp
for i,_ := range dp {
    dp[i] = make([]int,n)
}
// 填充列
for i:=0;i<m;i++{
    // dp[i] = make([]int, n)
    if obstacleGrid[i][0] == 1{
        dp[i][0] = 0
        break
    }
    dp[i][0] = 1
}
// 填充第一行为1
for i:=0;i<n;i++ {
    if obstacleGrid[0][i] == 1 {
        break
    }
    dp[0][i]=1
}

这里有一个坑，如果第一行或者第一列里面有障碍物的话，dp数组你怎么写

• 确定遍历顺序

dp[i][j] = dp[i – 1][j] + dp[i][j – 1] 中可以看出，要从左到右一层一层遍历，这样保证推导dp[i][j]的时候，
dp[i – 1][j] 和 dp[i][j – 1]有数值。

• 举例推导dp数组

[[0,0,0],[0,0,0],[1,0,0],[0,0,0]]
dp: [[1 1 1] [1 0 0] [0 0 0] [0 0 0]]

func uniquePathsWithObstacles2(obstacleGrid [][]int) int {
    m := len(obstacleGrid)
    n := len(obstacleGrid[0])
    dp := make([][]int, m)
    // 初始二维数组
    for i,_ := range dp {
        dp[i] = make([]int,n)
    }
    // 初始化
    for i:=0;i<m;i++ {
        // 如果是障碍物, 后面的就都是0, 不用循环了
        if obstacleGrid[i][0] == 1 {
            break
        }
        dp[i][0]=1
    }
    for i:=0;i<n;i++ {
        if obstacleGrid[0][i] == 1 {
            break
        }
        dp[0][i]=1
    }

    fmt.Println(dp)
    for i:=1;i<m;i++{
        for j:=1;j<n;j++{
            if obstacleGrid[i][j]!=1{
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
            }
        }
    }
    fmt.Println(dp)
    return dp[m-1][n-1]
}