分析步骤
- 确定dp数组(dp table)以及下标的含义
-
确定递推公式
-
dp数组如何初始化
-
确定遍历顺序
-
举例推导dp数组
———— 题解步骤来自博客
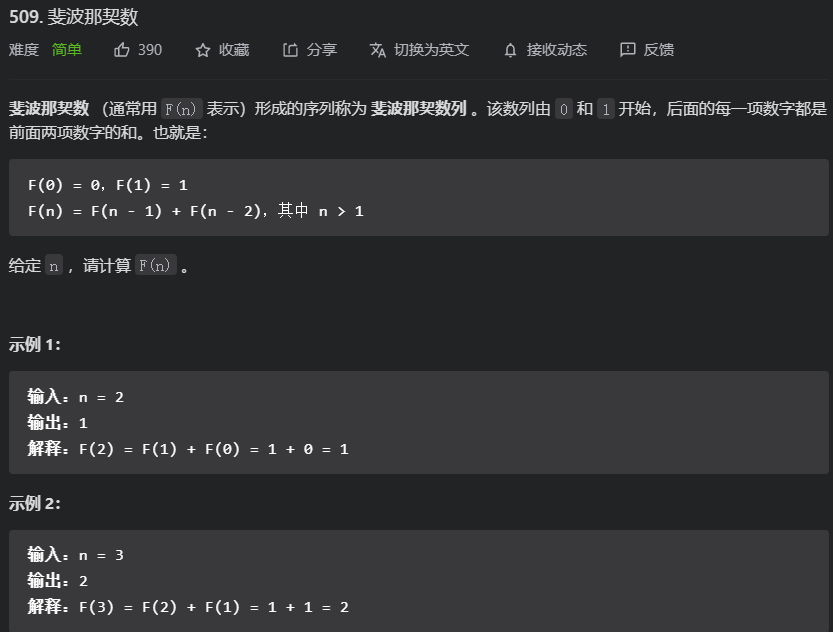
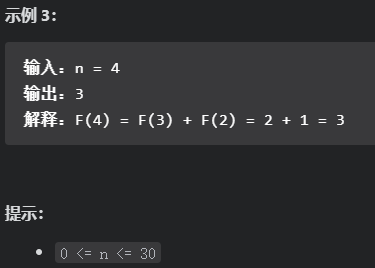
题目一
代码与解析
- 确定dp数组(dp table)以及下标的含义
dp用来记录每个斐波那契数 - 确定递推公式
题目中给了
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
- dp数组如何初始化
dp[0]=0
dp[1]=1
- 确定遍历顺序
dp[i]是依赖 dp[i – 1] 和 dp[i – 2],那么遍历应该是从前往后遍历 - 举例推导dp数组
eg: n=6
dp = [0,1,1,2,3,5,8]
func fib(n int) int {
if n==0{
return 0
}
dp := make([]int,n+1)
dp[0]=0
dp[1]=1
for i:=2;i<=n;i++{
dp[i]=dp[i-1]+dp[i-2]
}
return dp[n]
}
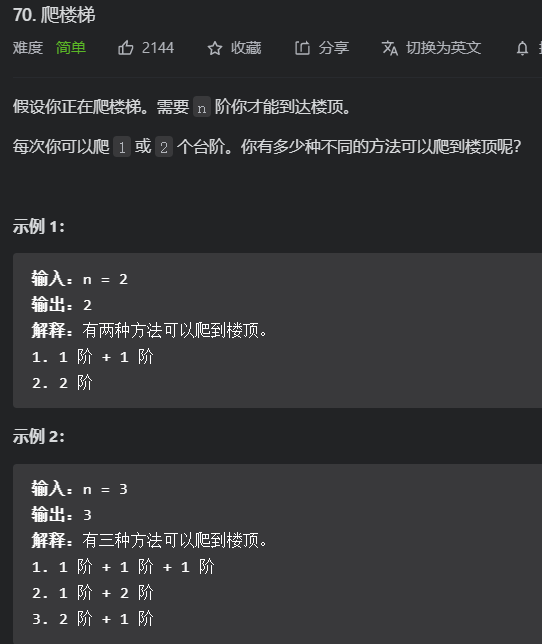
题目二
代码与解析
n=1 => 1
n=2 => 2:一次一步走两次, 一次两步
n=3 => 3:(1,1,1)(1,2)(2,1)
当前状态可以由前两个状态倒出来
carl大佬在博客详细解释了
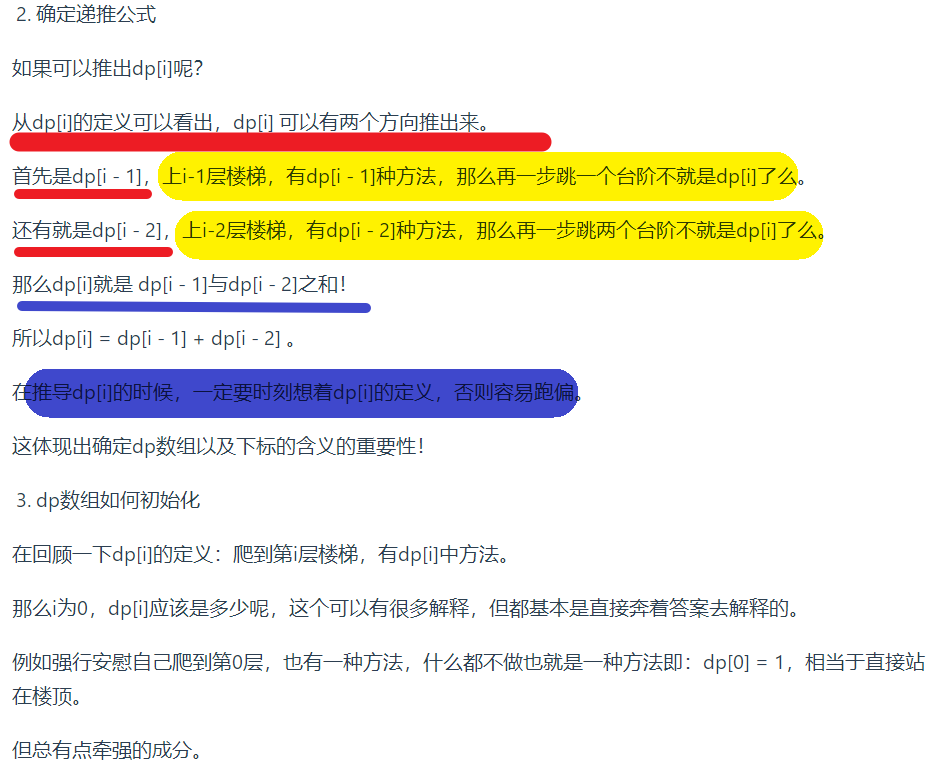
我理解的dp[0]是在地板上,不用动,地板即就是target
其余每一项的分析看上一题,代码很像
func climbStairs(n int) int {
if n==1{
return 1
}
dp:=make([]int,n+1)
dp[1]=1
dp[2]=2
for i:=3;i<=n;i++{
dp[i]=dp[i-1]+dp[i-2]
}
// fmt.Println(dp)
return dp[n]
}