文章导航
隐藏
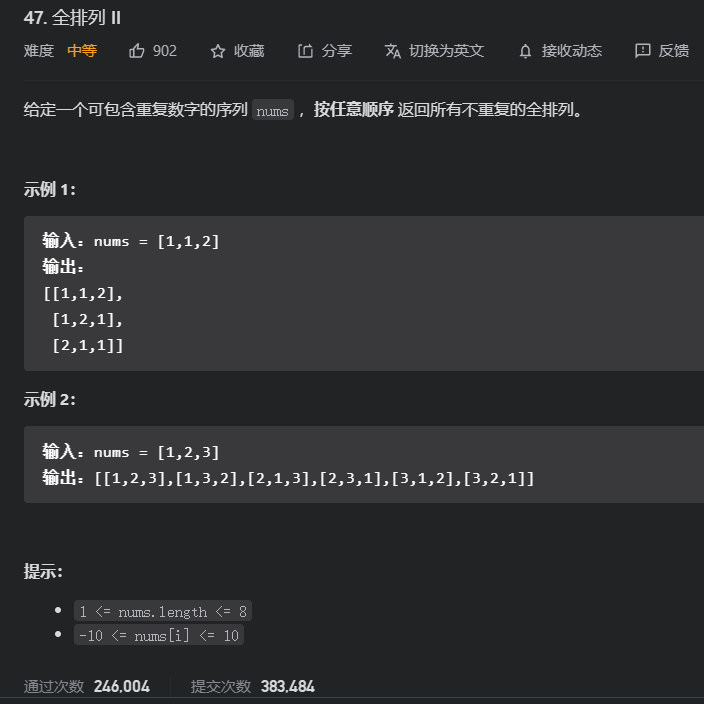
题目
代码与解析
这道题给定包含重复数字的序列,
要求返回所有不重复的全排列
我理解的这道题既要树层去重,也要树杈去重
至于树杈去重和https://blog.devilwst.top/2022/01/01/全排列-回溯/一样
还有一点,这道题一定要排序,
树层去重的话,我一开始想套模板:
// 下面这个代码在这道题里不行,和之前树层去重不同的是这道题是排列问题,排列问题不需要startIndex.
if i>startIndex&&nums[i]==nums[i-1]{
continue
}
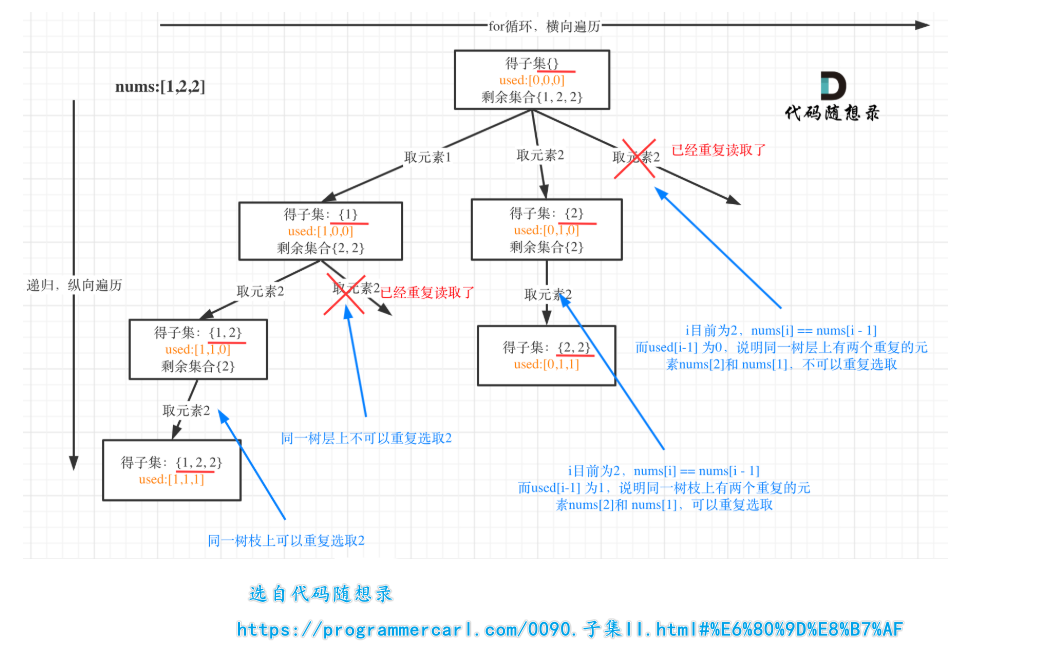
这道题里的去重问题还得看一下carl大佬的文章https://programmercarl.com/0090.子集II.
// 这里很容易迷糊
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
-----------------------------------------------------
// 而如果要对同一树层元素跳过进行去重的话,
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
// 下面必须撤销状态
used[i] = true;
// backtracking(nums, i + 1, used);
used[i] = false;
------------------------------------------------------
// 如果要对同一树杈元素去重的话
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
continue;
}
// 下面必须撤销状态
used[i] = true;
// backtracking(nums, i + 1, used);
used[i] = false;
------------------------------------------------------
——————思路摘自 carl大佬的 代码随想录
这道题的树杈去重我才用的和https://blog.devilwst.top/2022/01/01/全排列-回溯/同款解法

func permuteUnique(nums []int) [][]int{
res := [][]int{}
path := []int{}
sort.Ints(nums)
// used := map[string]bool{}
temUsed := make([]int, 21)
var backtracking func()
backtracking = func() {
if len(path) == len(nums) {
temp := make([]int, len(nums))
copy(temp, path)
res = append(res, temp)
return
}
for i := 0; i < len(nums); i++ {
if temUsed[i] == 1 {
continue
}
if i>0&&nums[i]==nums[i-1]&&temUsed[i-1]!=1{
continue
}
temUsed[i] = 1
path = append(path, nums[i])
backtracking()
path = path[:len(path)-1]
temUsed[i] = 0
}
}
backtracking()
return res
}
一种更笨拙,更简单的方式
这是我第一次提交的
我用了一个hash table来去重,用它存储每次path里的元素,并把类似“1,2,3”这样的元素做成字符串“123”,这样方便对比去重。

func permuteUnique(nums []int) [][]int {
res := [][]int{}
path := []int{}
used := map[string]bool{}
temUsed := make([]int, 21)
var backtracking func()
backtracking = func() {
if len(path) == len(nums) {
temp := make([]int, len(nums))
copy(temp, path)
key := ""
for _,k := range temp{
key += strconv.Itoa(k)
}
if ok, _ := used[key]; !ok {
used[key] = true
res = append(res, temp)
}
return
}
for i := 0; i < len(nums); i++ {
if temUsed[i] == 1 {
continue
}
temUsed[i] = 1
path = append(path, nums[i])
backtracking()
path = path[:len(path)-1]
temUsed[i] = 0
}
}
backtracking()
return res
}