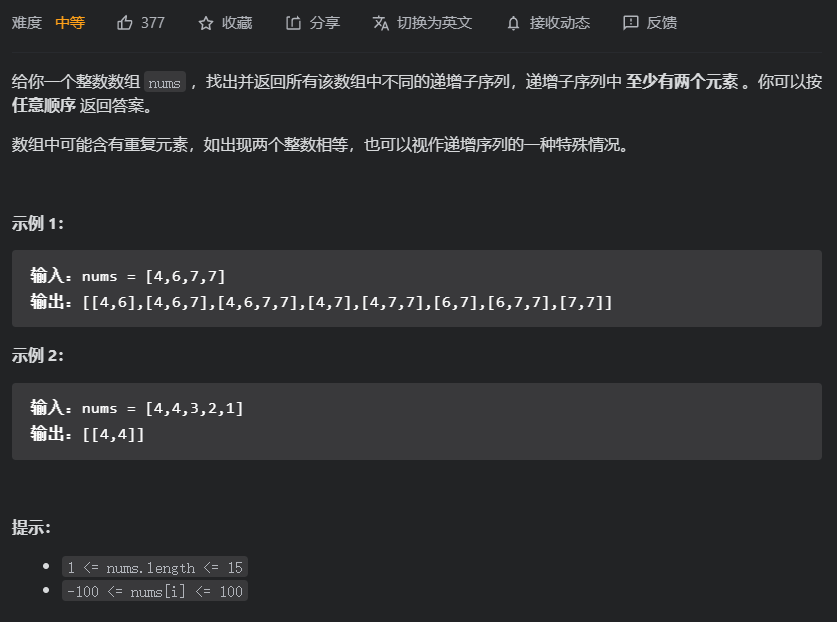
题目

leetcode:491

代码与解析

参考一：

题解中的这个视频讲解部分非常好，代码可以不用看

参考二：

这是carl大佬的讲解

注意题目中的几个点：

并且数组中可能包含重复元素，元素相等也是递增的一种情况，
递增子序列的长度>=2
这道题的一个坑就是，递增子序列， 不能自己手动给他进行排序。
这道题和https://blog.devilwst.top/2021/12/31/子集-回溯/不一样，这道题不能排序。不能使用之前的去重逻辑！！！！！！！！！

这道题和https://blog.devilwst.top/2022/01/01不同的是， 这道题要在一个树层中去重，而46题要在树杈中去重

回溯三部曲

• 确定递归参数及返回值
  要传入startIndex

• 确定终止条件
  因为要遍历整棵树，不用加return

if len(path)>=2{
    tem := make([]int, len(path))
    copy(tem, path)
    res = append(res, tem)
    // 这里不能加return ,因为要遍历整棵树
    // return 
}

• 确定单层逻辑
  注意：之前的去重逻辑不行， 因为这次数组不是有序的
  去重灵魂在这
  
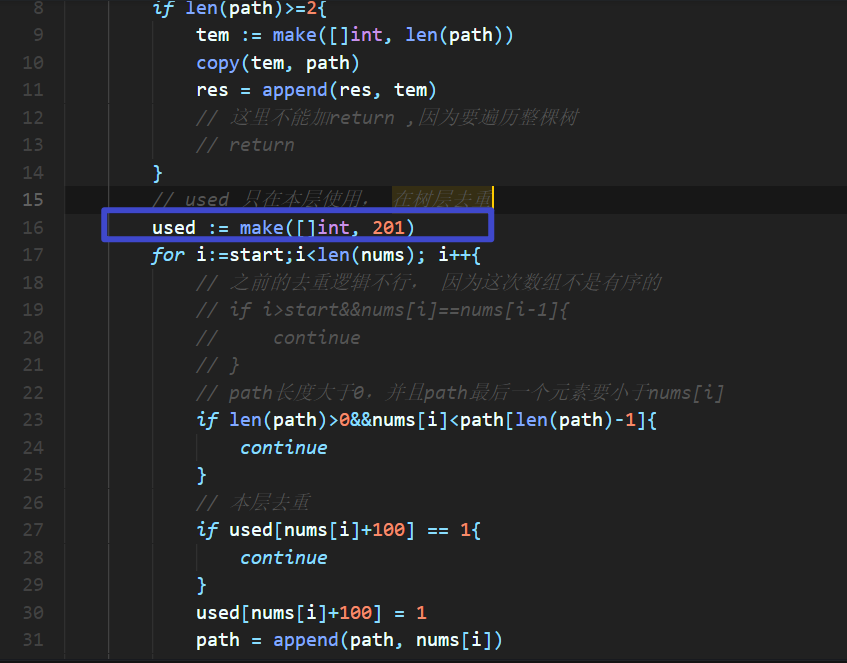
  nums[i]+100加100的原因是，

// 之前的去重逻辑不行， 因为这次数组不是有序的
    // if i>start&&nums[i]==nums[i-1]{
    //     continue
    // }

for i:=start;i<len(nums); i++{
    // 之前的去重逻辑不行， 因为这次数组不是有序的
    // if i>start&&nums[i]==nums[i-1]{
    //     continue
    // }
    // path长度大于0，并且path最后一个元素要小于nums[i]
    if len(path)>0&&nums[i]<path[len(path)-1]{
        continue
    }
    // 本层去重
    if used[nums[i]+100] == 1{
        continue
    }
    used[nums[i]+100] = 1
    path = append(path, nums[i])
    backtracking(i+1)
    path = path[:len(path)-1]
}

不是有序数组，树层去重代码略有不同：

func findSubsequences(nums []int) [][]int {
    res := [][]int{}
    path := []int{}
    // used := make([]int, 201) 这里加不行。
    var backtracking func(start int)
    backtracking = func(start int){
        if len(path)>=2{
            tem := make([]int, len(path))
            copy(tem, path)
            res = append(res, tem)
            // 这里不能加return ,因为要遍历整棵树
            // return 
        }
        // used 只在本层使用
        used := make([]int, 201)
        for i:=start;i<len(nums); i++{
            // 之前的去重逻辑不行， 因为这次数组不是有序的
            // if i>start&&nums[i]==nums[i-1]{
            //     continue
            // }
            // path长度大于0，并且path最后一个元素要小于nums[i]
            if len(path)>0&&nums[i]<path[len(path)-1]{
                continue
            }
            // 本层去重
            if used[nums[i]+100] == 1{
                continue
            }
            used[nums[i]+100] = 1
            path = append(path, nums[i])
            backtracking(i+1)
            path = path[:len(path)-1]
        }
    }
    backtracking(0)
    return res
}