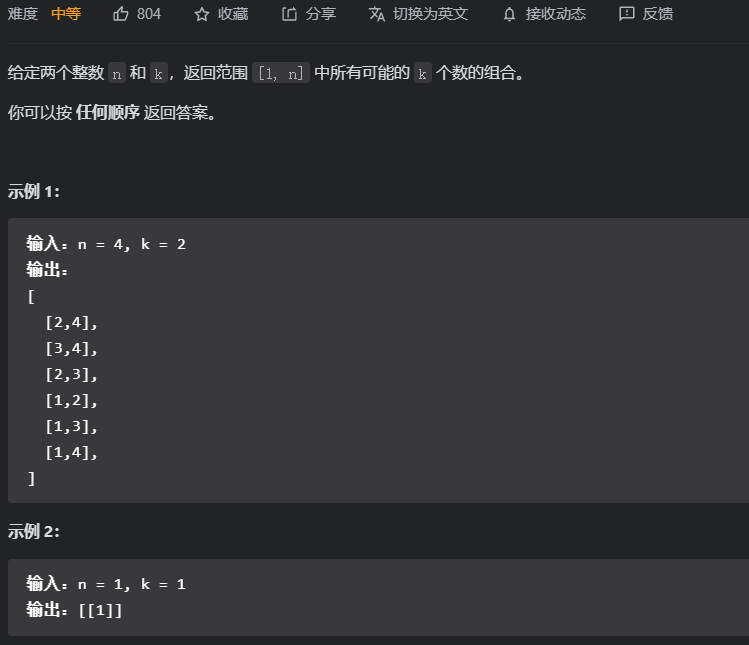
题目

leetcode:77

代码与解析

引用一下carl大佬的视频：
https://www.bilibili.com/video/BV1cy4y167mM回溯算法理论篇

https://www.bilibili.com/video/BV1wi4y157e回溯算法代码解析

https://www.bilibili.com/video/BV1wrtyi4y回溯算法剪枝
回溯法三部曲：

• 确定参数及返回值
  要传入start来记录下一层递归搜索的起始位置，path来记录符合条件的单一结果，不过不是必须的。

• 确定终止条件
  如果path长度等于k,说明满足条件，要把他转移到res, <注意这里必须要拷贝，不然path是一个指针，res里面的 结果将都是最后一个结果>

if len(path)==k{
    tmp := make([]int, k)
    copy(tmp, path)
    res = append(res, tmp)
    return
}

• 确定单层逻辑
  for循环做横向遍历， 递归做纵向遍历，另外别忘了加上回溯
  

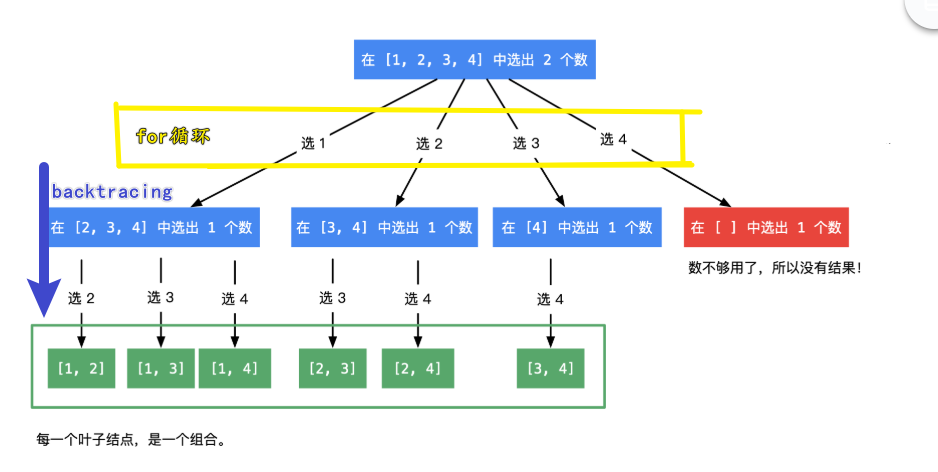
for i:=start;i<=n;i++{
    path = append(path, i)
    // 注意是i+1而不是start+1
    backtracing(i+1, path)
    path = path[:len(path)-1]
}

这里可以进行一个剪枝， 将哪些为空，或者不符合条件的 枝减去。
k-len(path)还剩这么多需要选取，n-(k-len(path))+1:这个表示至多要搜索的位置
具体讲解见carl大佬的视频：
https://www.bilibili.com/回溯剪枝：时间：8:28秒详解

for i:=start;i<=n-(k-len(path))+1;i++{
    path = append(path, i)
    // 注意是i+1而不是start+1
    backtracing(i+1)
    path = path[:len(path)-1]
}

完整代码：

func combine(n int, k int) [][]int {
    res := [][]int{}
    // path := []int{}
    var backtracing func (start int, path []int)
    backtracing = func (start int, path []int){
        if len(path)==k{
            tmp := make([]int, k)
            copy(tmp, path)
            res = append(res, tmp)
            return
        }
        for i:=start;i<=n-(k-len(path))+1;i++{
            path = append(path, i)
            // 注意是i+1而不是start+1
            backtracing(i+1, path)
            path = path[:len(path)-1]
        }

    }
    backtracing(1, []int{})
    return res
}
-----------------------精简版---------------------------
func combine(n int, k int) [][]int {
    res := [][]int{}
    var backtrack func(int, []int)
    backtrack = func(idx int, nums []int) {
        if len(nums) == k {
            t := make([]int, k)
            copy(t, nums)
            res = append(res, t)
            return
        }
        for i := idx; i <= n; i++ {
            backtrack(i + 1, append(nums, i))
        }
    }

    backtrack(1, []int{})
    return res
}