这两道题代码不复杂,但很绕,很考验对递归的理解
题目一
代码与解析
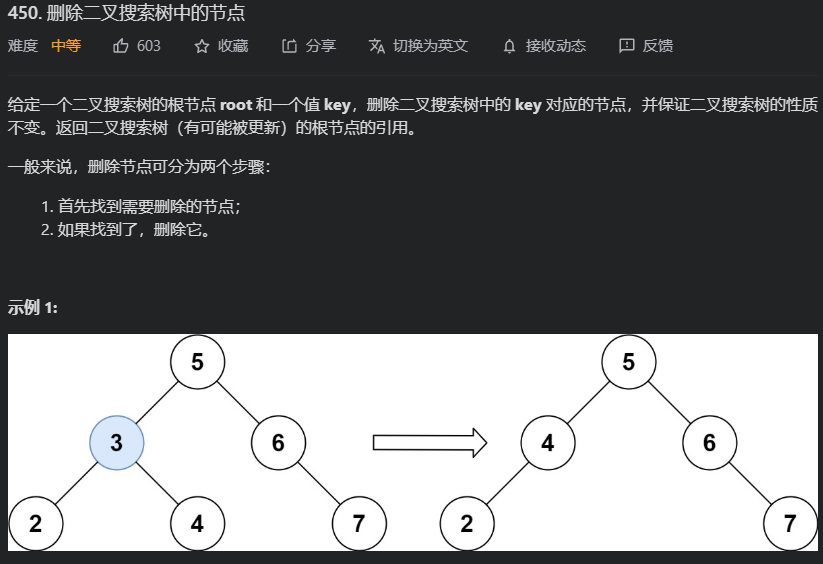
删除二叉搜索树节点可能需要调整结构,要保证删除之后仍然是一个二叉搜索树。
递归三部曲:
- 确定递归函数参数和返回值
要传入根节点和要删除节点key,返回左子树或右子树头结点指针 -
确定终止条件
if root==nil{
return nil
}
- 单层逻辑
if key < root.Val { // 如果要删除的值小于根节点的值
// 就递归去左子树上删除节点,并且返回的二叉树是当前根节点的左子树
root.Left = deleteNode(root.Left, key)
} else if key > root.Val { // 如果要删除的值大于根节点的值
// 就递归去右子树上删除节点,并且返回的二叉树是当前根节点的右子树
root.Right = deleteNode(root.Right, key)
} else { // 如果不是以上两种情况,说明要删除的值等于当前根节点的值
if root.Left == nil { // 先判断当前根节点是否只有一个子树
return root.Right // 是的话就返回那个唯一子树即可
} else if root.Right == nil {
return root.Left
}
// 下面这一段是把当前节点的右节点接到要删除节点的左结点之上,这样就是有序的了,见下图
rightMin := root.Right
for rightMin.Left != nil {
rightMin = rightMin.Left
}
rightMin.Left = root.Left
root = root.Right
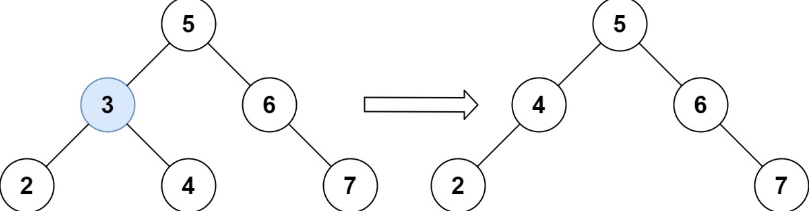
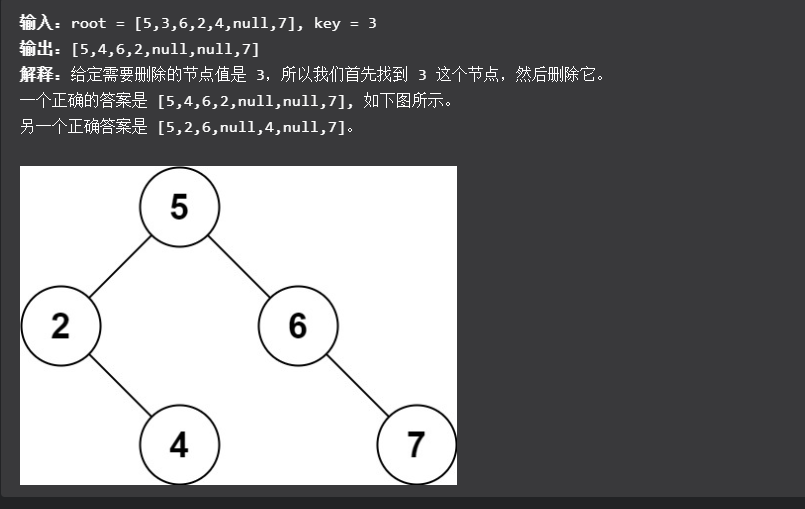
其实这和删除链表节点一个操作,先把后面的接上,然后再管前面的!!!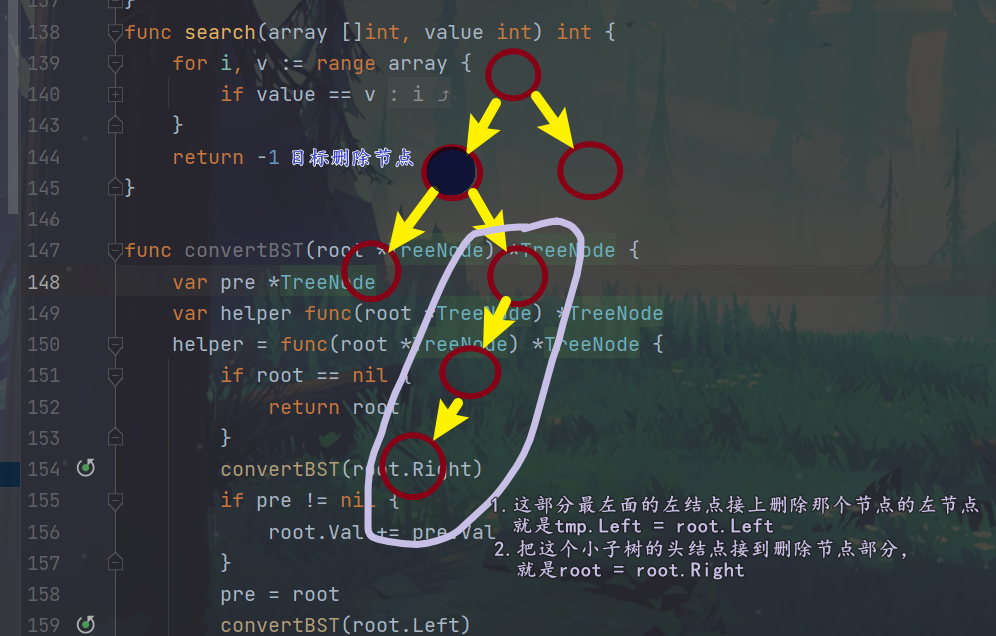
func deleteNode(root *TreeNode, key int) *TreeNode{
if root==nil{
return nil
}
if key<root.Val{
root.Left = deleteNode(root.Left, key)
}else if key>root.Val{
root.Right = deleteNode(root.Right, key)
}else{
if root.Left==nil{
return root.Right
}else if root.Right==nil{
return root.Left
}
tmp := root.Right
for tmp.Left!=nil{
tmp = tmp.Left
}
tmp.Left = root.Left
root = root.Right
}
return root
}
题目二
代码与解析
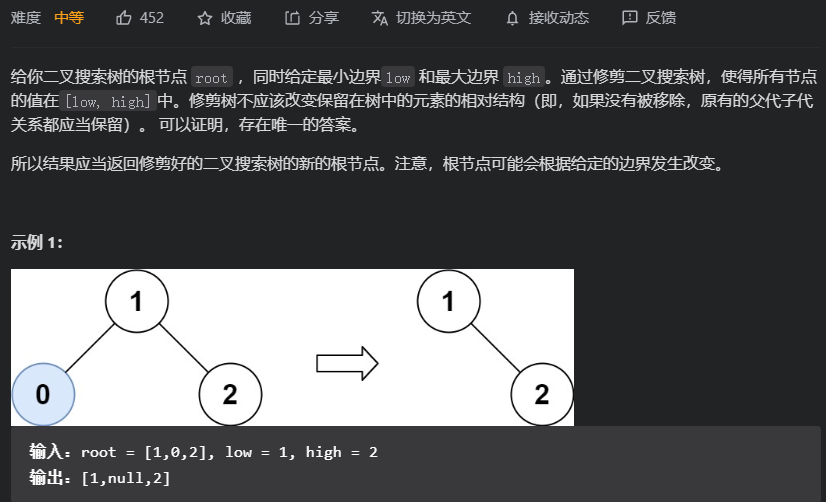
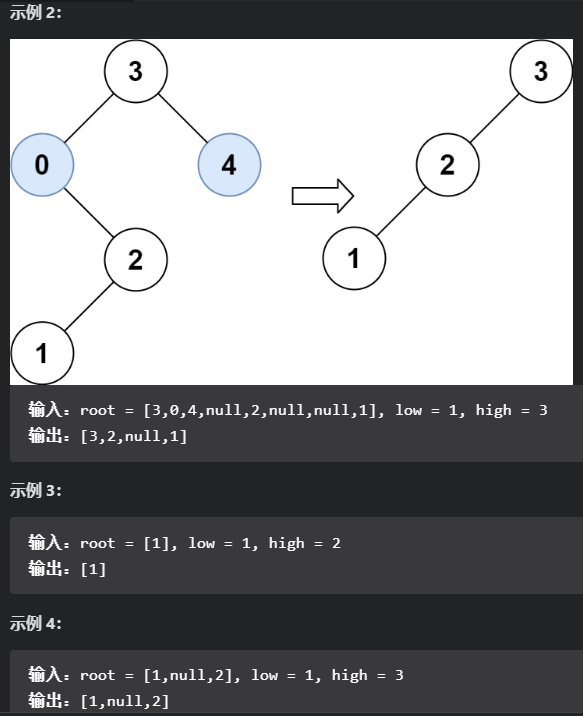
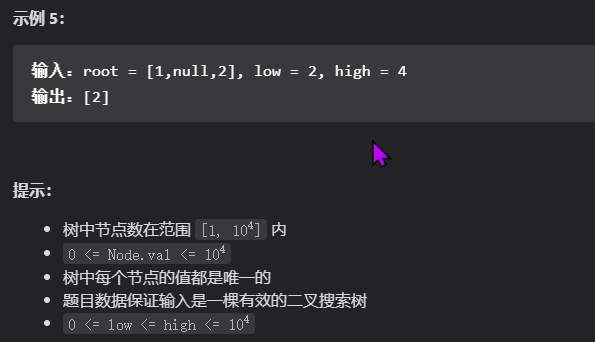
这道题不是单纯的移除一个节点,还要修剪,要保证修改完的二叉树是一个二叉搜索树。
递归三部曲
- 确定参数及返回值
要传入二叉树根节点,左区间,右区间,返回左子树,右子树的根节点
func trimBST(root *TreeNode, low int, high int) *TreeNode
- 确定终止条件
如果当前节点为空,返回 -
确定单层逻辑
// 确定搜索区间,快速确定范围
// 如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点。
if root.Val<low{
right := trimBST(root.Right, low, high)
return right
}
// 如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点。
if root.Val>high{
left := trimBST(root.Left, low, high)
return left
}
// 将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right。
root.Left = trimBST(root.Left, low, high)
root.Right = trimBST(root.Right, low, high)
就相当于这样
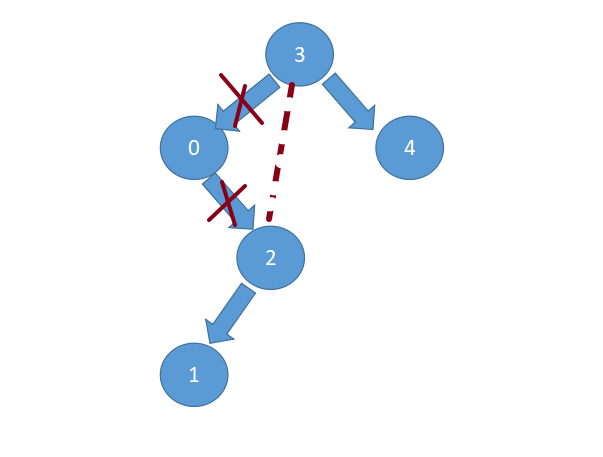
直接把0的右子树节点2返回给上一层,压根没管小于low那个边界的情况
func trimBST(root *TreeNode, low int, high int) *TreeNode {
if root==nil{
return root
}
if root.Val<low{
right := trimBST(root.Right, low, high)
return right
}
if root.Val>high{
left := trimBST(root.Left, low, high)
return left
}
root.Left = trimBST(root.Left, low, high)
root.Right = trimBST(root.Right, low, high)
return root
}