插播:
本段参考自carl大佬博客点此查看:
如果递归函数有返回值,怎么区分是搜索一条边还是整棵树
1搜索一条边
if(递归函数(root.Left)){
return
}
if (递归函数(root.Right)){
return
}
2搜索整棵树
left := 递归函数(root.Left)
right := 递归函数(root.Right)
在递归函数有返回值的情况下:
- 如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,
-
如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
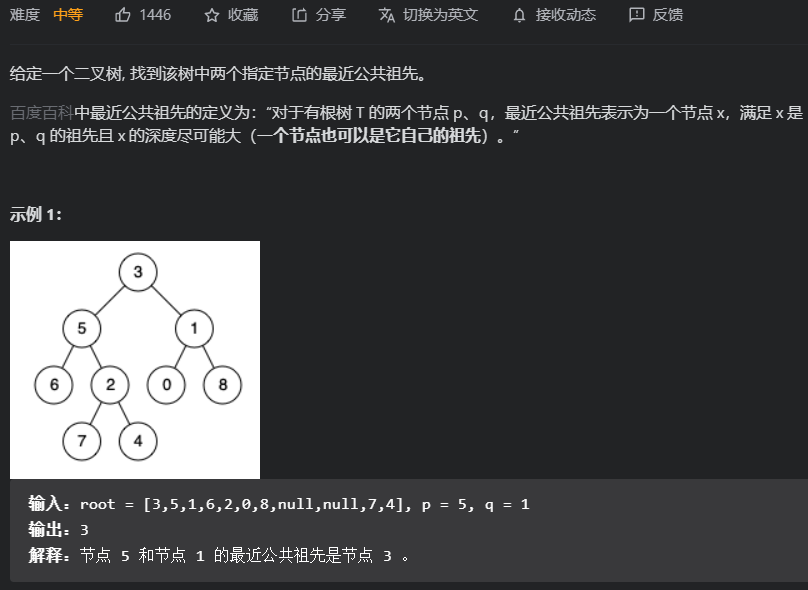
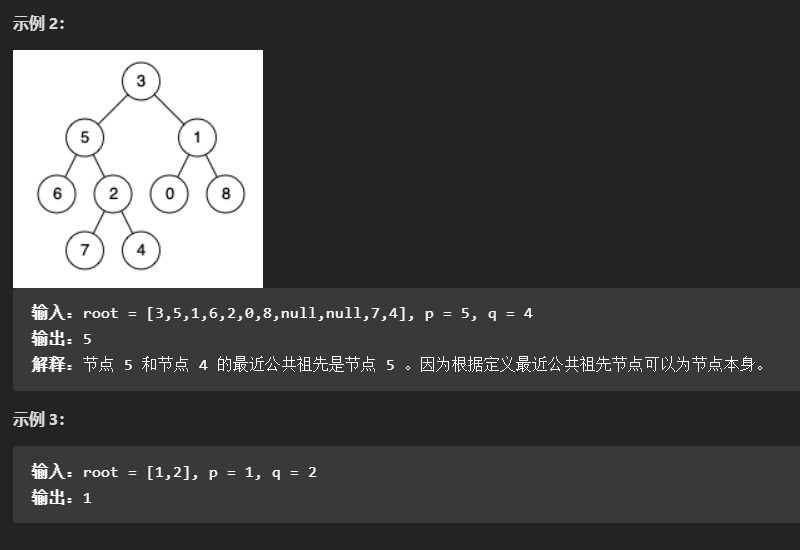
题目一
代码与解析
这道题要从底往上查找,回溯就是从底往上,
而后序遍历就是天然的回溯过程,最先处理的一定是叶子结点
如果一个节点的左子树等于p,右节点等于q,或者相反,那么该节点就是公共节点
递归三部曲:
- 确定函数参数及返回值
要传入root, p, q, 返回需要的节点。如果遇到p,q就把p,q返回 -
确定终止条件
if root==nil{
return root
}
if root==p||root==q{
return root
}
- 确定单层递归逻辑
分别用left和right接受递归的参数,然后处理left, right
if left!=nil&&right!=nil{
return root
}
// 如果左面不为空,右为空,那么说明是从左边路径返回的
if left!=nil{
return left
}
// 如果右面不为空,左为空,那么说明是从右边路径返回的
if right!=nil{
return right
}
整体代码:
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root==nil{
return root
}
if root==p||root==q{
return root
}
// 是遍历整棵树,所以用left, right接受
left:=lowestCommonAncestor(root.Left, p, q)
right:=lowestCommonAncestor(root.Right, p, q)
if left!=nil&&right!=nil{
return root
}
// 如果左面不为空,右为空,那么说明是从左边路径返回的
if left!=nil{
return left
}
// 如果右面不为空,左为空,那么说明是从右边路径返回的
if right!=nil{
return right
}
return nil
}
题目二
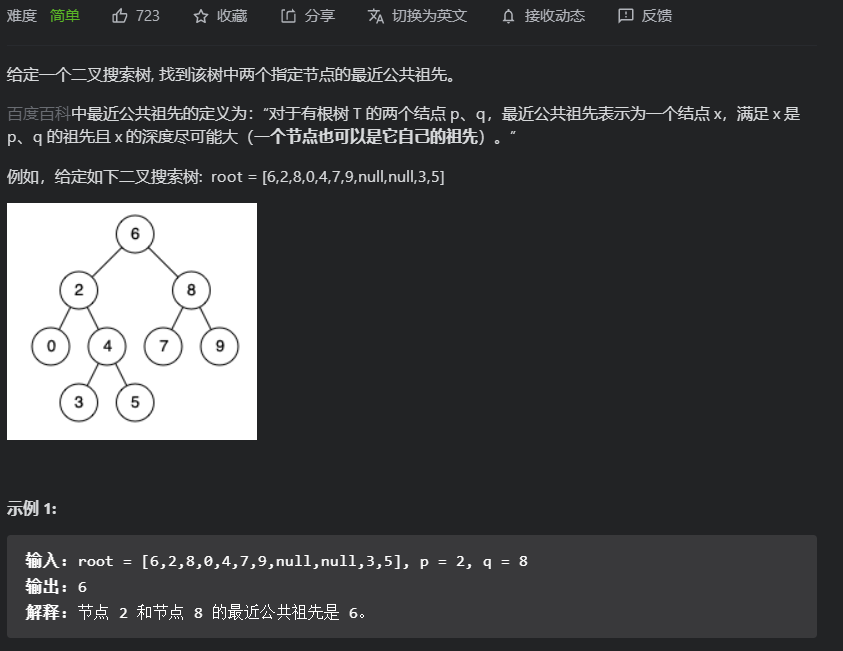

代码与解析二
这道题也可以用普通二叉树那样的方式,
不过那样就完全没用上二叉搜索树这个条件
递归三部曲:
- 确定参数及返回值
要传入root, p, q,
返回最近 的公共祖先 -
确定终止条件
if root==nil{
return root
}
其实这个条件不用,题目中说了,不存在空。
- 确定单层逻辑
在遍历二叉搜索树的时候就是寻找区间[p.Val, q.Val](是左闭又闭)
那么如果 cur.Val 大于 p.Val,同时 cur.Val 大于q.Val,就应该向左遍历(说明目标区间在左子树上)。
相反在右子树上。

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root==nil{
return root
}
if root.Val>p.Val&&root.Val>q.Val{
return lowestCommonAncestor(root.Left, p,q)
}else if root.Val<p.Val&&root.Val<q.Val{
return lowestCommonAncestor(root.Right,p,q)
}else{
return root
}
}