题目
1.二叉树种类
- 满二叉树
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
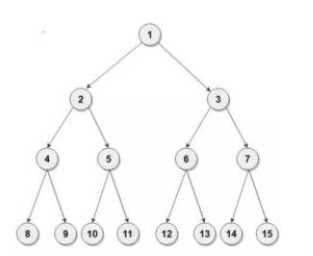
- 完全二叉树
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^h -1 个节点。
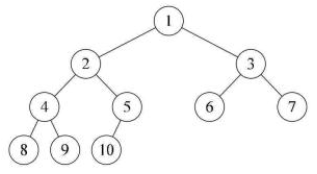
- 二叉搜索树
二叉搜索树是一个有数值的树,是一个有序树。 - 平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两棵子树都是一棵平衡二叉树。
2.遍历方式
- 深度优先
Go版(递归)
2.1前序遍历
// preorderTraversal 前序遍历
func preorderTraversal(root *TreeNode) (res []int) {
var traversal func(node *TreeNode)
traversal = func(node *TreeNode) {
if node == nil {
return
}
res = append(res, node.Val)
traversal(node.Left)
traversal(node.Right)
}
traversal(root)
return res
}
2.2中序遍历
// inorderTraversal 中序遍历
func inorderTraversal(root *TreeNode) (res []int) {
var traversal func(node *TreeNode)
traversal = func(node *TreeNode) {
if node == nil {
return
}
traversal(node.Left)
res = append(res, node.Val)
traversal(node.Right)
}
traversal(root)
return res
}
2.3后序遍历
// postorderTraversal 后序遍历
func postorderTraversal(root *TreeNode) (res []int) {
var traversal func(node *TreeNode)
traversal = func(node *TreeNode) {
if node == nil {
return
}
traversal(node.Left)
traversal(node.Right)
res = append(res, node.Val)
}
traversal(root)
return res
}
Go版——迭代(非递归)
1.前序遍历
// 前序遍历
// preorderTraversal 非递归遍历,迭代遍历
// 前序遍历
func preorderTraversal2(root *TreeNode) (res []int) {
if root == nil {
return res
}
stack := list.New()
stack.PushBack(root)
for stack.Len() > 0 {
// stack.Back()返回最后一个元素,而且这里必须做类型断言
node := stack.Remove(stack.Back()).(*TreeNode)
//fmt.Printf("%T:", node)
res = append(res, node.Val)
if node.Right != nil {
stack.PushBack(node.Right)
}
if node.Left != nil {
stack.PushBack(node.Left)
}
}
return res
}
2.后序遍历
// 后序遍历
func postorderTraversal2(root *TreeNode) (res []int) {
stack := list.New()
if root == nil {
return res
}
stack.PushBack(root)
for stack.Len() > 0 {
node := stack.Remove(stack.Back()).(*TreeNode)
res = append(res, node.Val)
if node.Left != nil {
stack.PushBack(node.Left)
}
if node.Right != nil {
stack.PushBack(node.Right)
}
}
reverse(res)
return res
}
func reverse(res []int) {
left, right := 0, len(res)-1
for right > left {
res[left], res[right] = res[right], res[left]
left++
right--
}
}
3.中序遍历
// 中序遍历:左中右
func inorderTraversal2(root *TreeNode) (res []int) {
if root == nil {
return res
}
cur := root
stack := list.New()
// 使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素
for cur != nil || stack.Len() > 0 {
if cur != nil {
// 只要当前cur不为空,就把当前节点添加进栈,
stack.PushBack(cur)
// 然后一直遍历
cur = cur.Left
} else {
// 如果当前节点为空,那么就从栈弹出元素
cur = stack.Remove(stack.Back()).(*TreeNode)
// 然后节点添加进返回的数组
res = append(res, cur.Val)
//然后再继续遍历
cur = cur.Right
}
}
return res
}
python版
2.4前序遍历
class Solution:
def preordertraversal(self, root:TreeNode)->List[int]:
res = []
def traversal(root:TreeNode):
if root==None:
return
res.append(root.val)
traversal(root.left)
traversal(root.right)
traversal(root)
return res
2.5中序遍历
class Solution:
def inordertraversal(self, root:TreeNode)->List[int]:
res = []
def traversal(root:TreeNode):
if root==None:
return
traversal(root.left)
res.append(root.val)
traversal(root.right)
traversal(root)
return res
2.6后序遍历
class Solution:
def postordertraversal(self, root:TreeNode):
res = []
def traversal(root:TreeNode):
if root==None:
return
traversal(root.left)
traversal(root.right)
res.append(root.val)
traversal(root)
return res
- 广度优先



