1.KMP
是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配。
1.1前缀表
前缀表(prefix table)记录的是但模式串与主串不匹配的时候,模式串应从哪里重新匹配

// 前缀表 next数组
// i:后缀表末尾 j:前缀表末尾
next := make([]int, len(needle))
fmt.Println(next)
j := 0 // 前缀表末尾初始化
for i := 1; i < len(needle); i++ {
// 末尾不相等的情况
//fmt.Println("needle[i]:", string(needle[i]), "needle[j]:", string(needle[j]))
for j > 0 && needle[j] != needle[i] {
j = next[j-1]
//fmt.Println(j)
}
if needle[i] == needle[j] {
j++
next[i] = j
}
}
1.2匹配
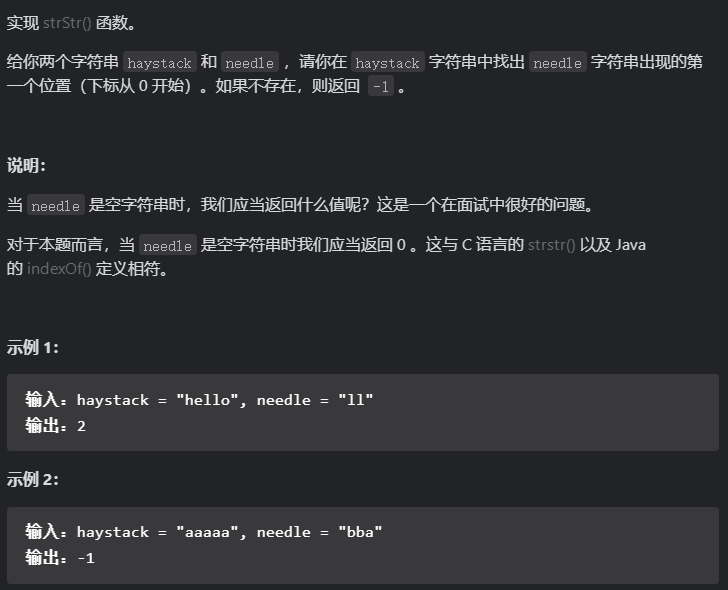
在文本串haystack里 找是否出现过模式串needle。
定义两个下标j 指向模式串起始位置,i指向文本串起始位置。
那么j初始值依然为0, 依然因为next数组里记录的起始位置为0,i和生成next数组时候不同了,这时候他要从0开始。
func strStr(haystack string, needle string) int {
if len(needle) == 0 {
return 0
}
next := make([]int, len(needle))
getNext(next, needle)
j := -1 // 模式串的起始位置 next为-1 因此也为-1
for i := 0; i < len(haystack); i++ {
// 处理不相等
for j > 0 && haystack[i] != needle[j+1] {
j = next[j-1] // 寻找下一个匹配点
}
// 处理相等,相等的时候模式串里索引加一
if haystack[i] == needle[j] {
j++
}
if j == len(needle)-1 { // j指向了模式串的末尾
return i - len(needle) + 1
}
}
return -1
}
2.题目1

3.题解与分析
func strStr(haystack string, needle string) int {
// j:前缀末尾 i:后缀末尾
j := 0
// 初始化前缀表数组
next := make([]int, len(needle))
for i := 1; i < len(needle); i++ {
// 处理不相等的情况
for needle[j] != needle[i] && j > 0 {
j = next[j-1]
}
// 处理相等的情况
if needle[i] == needle[j] {
j++
next[i] = j
}
}
j = 0
if len(needle) == 0 {
return 0
}
fmt.Println(next)
for i := 0; i < len(haystack); i++ {
// 处理不相等
for j > 0 && needle[j] != haystack[i] {
j = next[j-1]
}
// 处理相等
if needle[j] == haystack[i] {
j++
}
if j == len(needle) {
return i - len(needle) + 1
}
}
return -1
}
// getNext 构造前缀表next
// params:
// next 前缀表数组
// s 模式串
func getNext(next []int, s string) {
j := 0
next[0] = j
for i := 1; i < len(s); i++ {
for j > 0 && s[i] != s[j] {
j = next[j-1]
}
if s[i] == s[j] {
j++
}
next[i] = j
}
}
func strStr(haystack string, needle string) int {
n := len(needle)
if n == 0 {
return 0
}
j := 0
next := make([]int, n)
getNext(next, needle)
for i := 0; i < len(haystack); i++ {
for j > 0 && haystack[i] != needle[j] {
j = next[j-1] // 回退到j的前一位
}
if haystack[i] == needle[j] {
j++
}
if j == n {
return i - n + 1
}
}
return -1
}
题目2
分析与题解
这是一道标准的kmp题目
next 数组记录的就是最长相同前后缀
至于怎么判断呢?
数组长度÷ (数组长度-最长相同前后缀长度)判断是否可以整除,可以整除&&最长相同前后缀!=0,那么返回true
数组长度 – 最长相同前后缀的长度 相当于是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。

func repeatedSubstringPattern(s string) bool {
if len(s)<=1{
return false
}
next := make([]int, len(s))
j := 0
// 前缀表末尾j, 后缀表末尾i
for i:=1;i<len(s);i++{
// 不相等
for j>0&&s[j]!=s[i]{
j = next[j-1]
}
// 相等
if s[i]==s[j]{
j++
next[i] = j
}
}
// 判断前缀表末尾与字符串长度关系
n := len(s)
judge := n%(n-next[n-1])
if judge==0&&next[n-1]!=0{
return true
}
return false
}