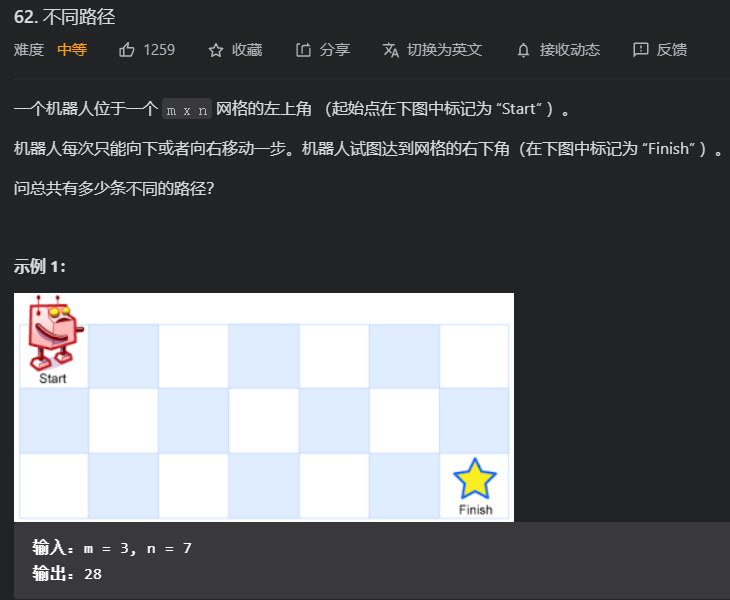
题目
代码与解析
动归五部曲
- 确定dp数组和下标含义
dp是一个二维数组,可以理解为存的这样一张图

dp[i][j]表示从(0,0)出发到达(i, j)有多少条路径
- 确定递推公式

看图, 图截取自视频力抠题解
比如第二行第二列的2 等于他的正上方和他的左方之和
换做公式就是:dp[i][j] = dp[i-1][j] + dp[i][j-1]
- dp数组初始化
按照上方图将dp初始化,并把第一行和第一列填1
dp := make([][]int, m)
// fmt.Println(dp) [[] [] []]
for i := range dp {
dp[i] = make([]int, n) // 初始化二维数组里的一维数组
dp[i][0] = 1 // 将二维数组第一列填1
}
// fmt.Println(dp) [[1 0 0 0 0 0 0] [1 0 0 0 0 0 0] [1 0 0 0 0 0 0]]
for j := 0; j < n; j++ {
dp[0][j] = 1 // 第一行填充1
}
// fmt.Println(dp) [[1 1 1 1 1 1 1] [1 0 0 0 0 0 0] [1 0 0 0 0 0 0]]
- 确定遍历顺序
dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
- 举例列出dp数组

[[1 1 1 1 1 1 1] [1 2 3 4 5 6 7] [1 3 6 10 15 21 28]]
func uniquePaths(m int, n int) int {
dp := make([][]int, m)
// fmt.Println(dp) [[] [] []]
for i := range dp {
dp[i] = make([]int, n) // 初始化二维数组里的一维数组
dp[i][0] = 1 // 将二维数组第一列填1
}
// fmt.Println(dp) [[1 0 0 0 0 0 0] [1 0 0 0 0 0 0] [1 0 0 0 0 0 0]]
for j := 0; j < n; j++ {
dp[0][j] = 1 // 第一行填充1
}
// fmt.Println(dp) [[1 1 1 1 1 1 1] [1 0 0 0 0 0 0] [1 0 0 0 0 0 0]]
// 根据递推公式算
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
dp[i][j] = dp[i-1][j] + dp[i][j-1]
}
}
fmt.Println(dp)
return dp[m-1][n-1]
}
用一维数组,方法很巧,不记录每一个位置
func uniquePaths(m int, n int) int {
dp := make([]int, n)
// 初始化数组
for i:=range dp{
dp[i] = 1
}
// 递推公式
for i:=1;i<m;i++{
for j:=1;j<n;j++{
dp[j] = dp[j-1] + dp[j]
}
}
// fmt.Println(dp)
return dp[n-1]
}