题目一
代码与解析一
没想出来

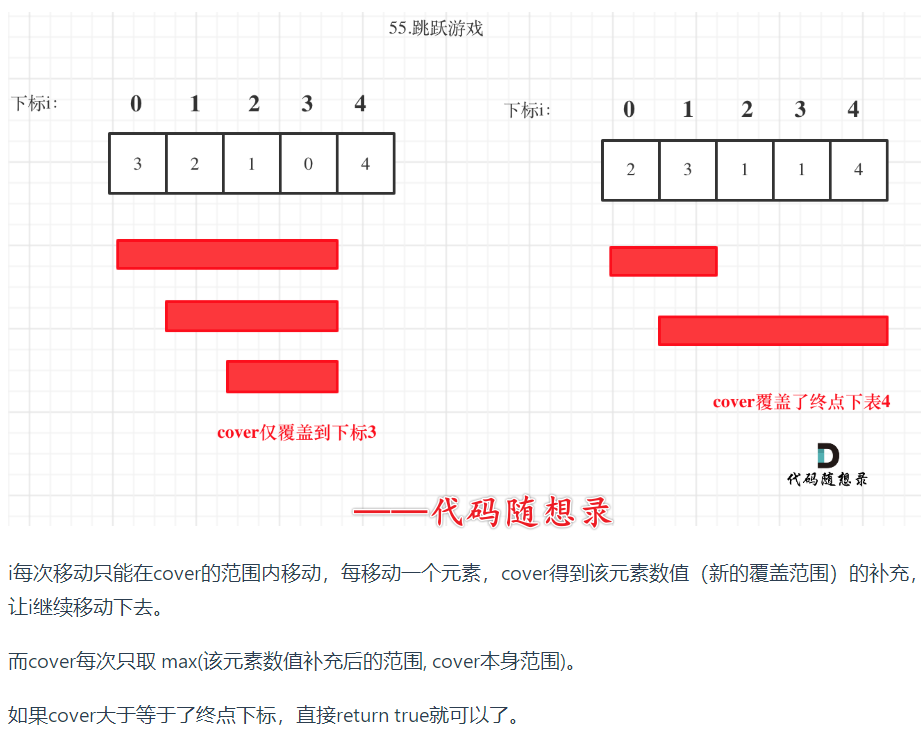
原文链接: 跳跃游戏.
贪心算法:
局部最优:每次取最大跳跃步数,最大覆盖范围。
整体最优:最后得到的整体最大覆盖范围能否到达终点
for循环: i每次在cover范围内移动,每移动一次,就更新一次cover覆盖范围,让他继续移动。
func canJump(nums []int) bool {
cover := 0
if len(nums)==1{
return true
}
// 主体, 、
// for循环
for i:=0;i<=cover;i++{
// 每次更新cover
cover = max(nums[i]+i, cover)
if cover>=len(nums)-1{
return true
}
}
return false
}
// 求最值
func max(x, y int)int{
if x>y{
return x
}else{
return y
}
}
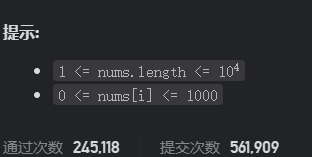
题目二
代码与解析二
没想出来
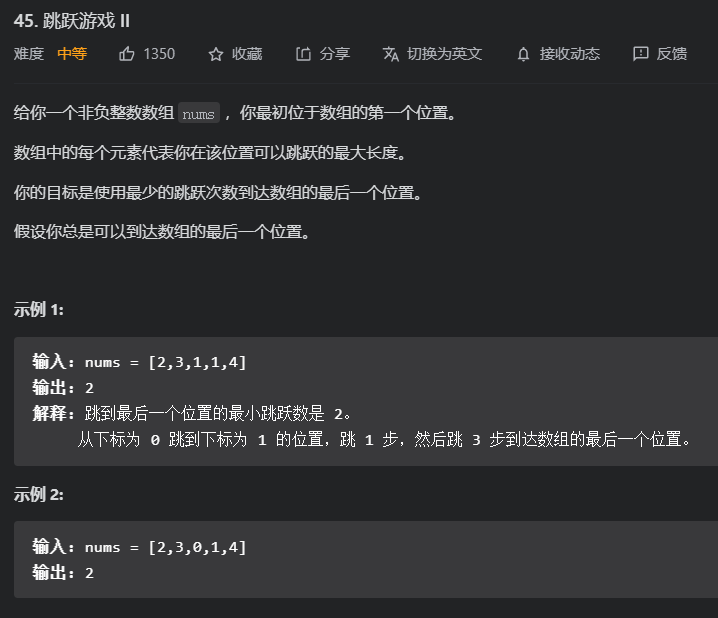
本题是假设肯定能到达最后一个位置,要用最少的步数跳到
贪心:
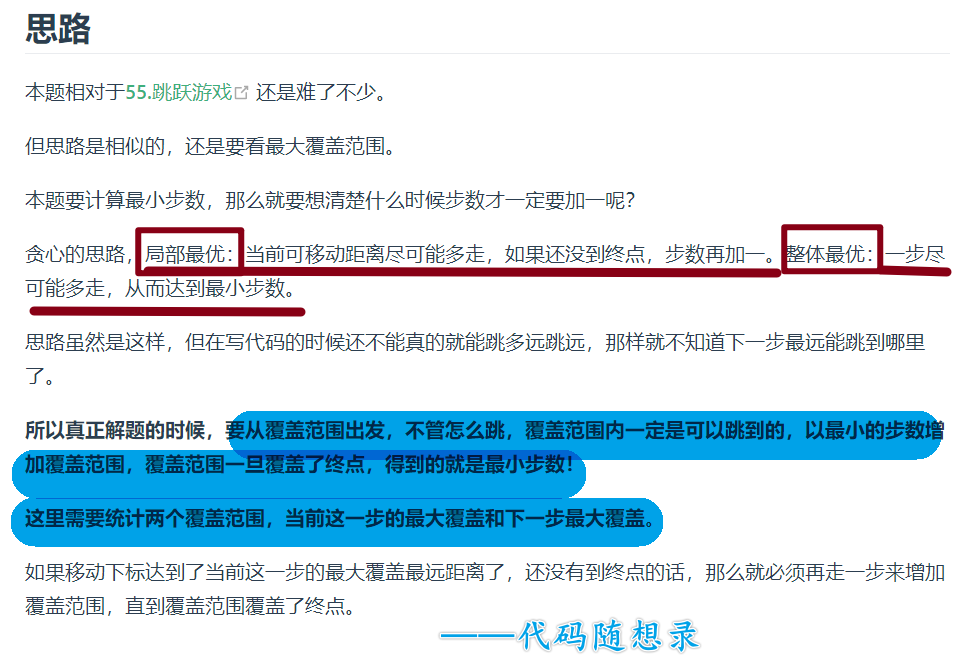
局部最优:当前移动距离尽可能多走,没到终点,步数就+1
整体最优:一步尽可能多走,步数最少
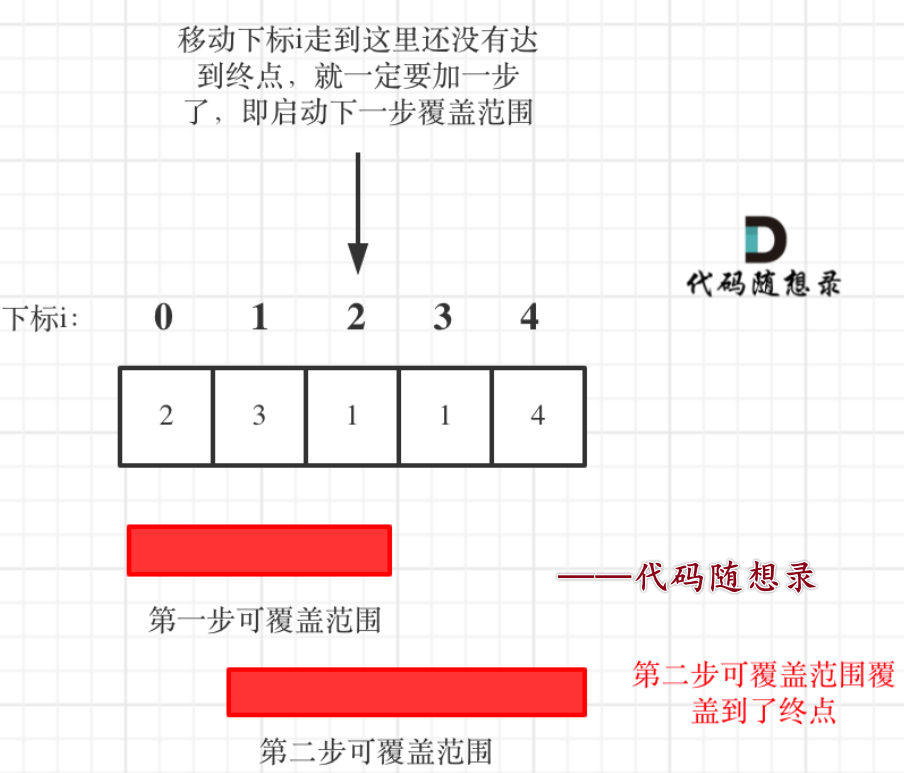
图中覆盖范围的意义在于,只要标为红色的区域,最多两步一定可以到!不管怎么走
func jump(nums []int) int {
min := 0
// count := 0
cur := 0 // 当前覆盖最远距离下标
next := 0 // 下一步覆盖最远距离下标
for i:=0;i<len(nums)-1;i++{
next = max(nums[i] + i, next) // 更新下一步覆盖最远距离下标
if cur==i{ // 遇到当前覆盖最远距离下标
if cur!=len(nums)-1{ // 如果当前覆盖最远距离下标不是终点
min++ // 如果当前覆盖最远距离下标不是终点
cur = next // 更新当前覆盖最远距离下标
if next>=len(nums)-1{ // 下一步的覆盖范围已经可以达到终点,结束循环
break
}
}else{
break
}
}
}
return min
}
func max(x, y int)int{
if x>y{
return x
}else{
return y
}
}